賽伊法則(英語:Say's Law),也稱作賽伊市場定律(Say's Law Of Market)或市場定律(Law of Markets),是一種在19世紀初流行的經濟思想定律,此定律被提出來的時間點是在工業革命之後,在一個完全賣方主導的市場,這種情境下賽伊法則是成立的。因為產品總是用產品(貨幣)來購買,買者同時也就是賣者,買賣是完全一致的。
對了說到買賣(maimai)

maimai(日語:maimai(マイマイ)),中國大陸版本稱舞萌,是一款由SEGA開發的大型電玩音樂遊戲,最早於2012年7月11日開始在日本營運,並於後期擴充至全球市場。(以下略)
大家應該都知道nowob很喜歡打mai,而nowob剛入坑就一直覺得maimai的刷圈特別帥,他也認為只要能夠刷圈刷得夠強那旁人肯定會覺得他很帥(但這顯然是他的妄想,路人大概只覺得他是傻逼)
而為了能夠帥氣的刷圈,nowob努力的學習刷圈知識,想知道每次刷圈可以拿多少分
不過他並不聰明,你可以依照以下指示寫個程式幫助他嗎?
(這台maimai來自平行宇宙,所以規則跟我們宇宙的maimai有點差別,避免玩過的人寫太快:0)
你在一個有 8 個等分按鍵的圓環上進行刷圈操作,使用左右兩隻手,但每回合只能選一隻手刷圈
圓環如圖(我用小畫家畫得很醜見諒)
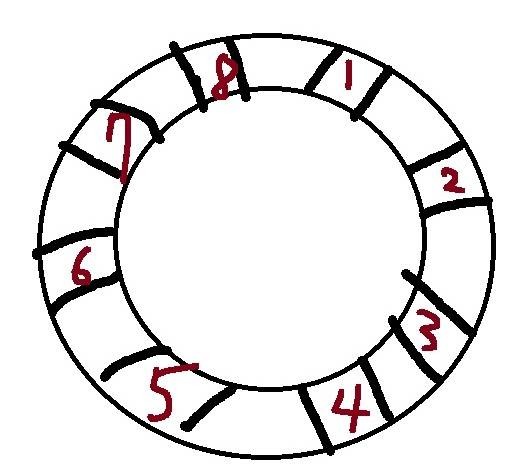
每次nowob可以選擇要用哪隻手刷圈以及要刷幾顆鍵還有要順時針還是逆時針(用刷幾顆鍵的正負數表示方向)
圓環上的每個按鍵有一個小寫字母標記 $\mathbf{a}$ ~ $\mathbf{z}$,分別表示八顆按鍵可以拿到的分數$\mathbf{a} = {1}$ , $\mathbf{b} = {2}$ ... $\mathbf{z} = {26}$ 以此類推
每次nowob刷完圈都會把這次路徑上的所有分數加總
而每隻手都會有自己的combo數,初始皆為$\mathbf{1}$
假設這次刷右手跟上次刷右手的方向一樣,那combo + $\mathbf{1}$,否則設回$\mathbf{1}$
combo數用來表示這回合可以乘上的數字
例如:nowob連續三次左手都刷同一個方向 分別原始分數累積$\mathbf{3}$ , $\mathbf{4}$ , $\mathbf{5}$ 最後實際分數是$\mathbf{3}$ + $\mathbf{8}$ + $\mathbf{15}$ ,而無論中間穿了多少次右手,左手的combo數都不會改變,也可以說左右手的計算是各自獨立的
兩手位置皆以 1-based 表示,則初始時左、右手位置皆為 $\mathbf{1}$
而假如這回合刷了$\mathbf{0}$ (沒刷) 那combo保持不變
每次的初始位置都是$\mathbf{1}$
同時為了避免nowob一次刷太多分,只要刷超過一圈分數都只算一圈
(意思是假如這次刷的按鍵數超過8 分數以刷了8顆計算)
(詳請可見下面範例說明)
第一行:$\mathbf{k}$ 表示刷幾次
第二行:一個長度為 $\mathbf{8}$ 的字串 $S$ 表示八個按鍵的分數(保證為小寫)
接下來 $\mathbf{k}$ 行:每行兩個整數 $\mathbf{h}$ , $\mathbf{d}$,表示本回合使用的手($\mathbf{1}$ 左手、$\mathbf{2}$ 右手)與該手位移量 $d$
輸出一個整數:所有回合分數的總和。
範例一: 3 abcdefgh 1 3 2 -2 1 9 範例二: 1 zzzzzzzz 2 -100 範例三: 2 aaaabbbb 1 4 1 2 範例四: 6 abcdefgh 1 3 2 -2 1 -4 2 5 1 1 2 -1
範例一: 96 範例二: 208 範例三: 13 範例四: 60
公開 測資點#0 (50%): 1.0s , <1M
公開 測資點#1 (50%): 1.0s , <10M
每次刷圈的起點不用計分
每次刷圈只要超過一圈( > |8| ) 分數就只要算一圈的分數
$1 \le \mathbf{k} \le 2\times 10^5$
$-10^9 \le d \le 10^9$
$\mathbf{50}$% : 對每一隻手,任兩次該手出現時的位移方向必定相反(不用記combo,可參考範例四)
$\mathbf{50}$% : 無額外限制
範例說明:
範例一:
第一次刷圈:左手 d=+3,路徑是 2,3,4,原始分數=2+3+4=9。左手第一次動,combo=1 → 得 9。
第二次刷圈:右手 d=-2,路徑是 8,7,原始分數=8+7=15。右手第一次動,combo=1 → 得 15。
第三次刷圈:左手 d=+9(≥8 當成全圈),原始分數=1+…+8=36。方向跟上次左手相同,所以左手 combo 變 2 → 得 36×2=72。
總分 9+15+72=96。
範例二:
只刷一次,|d|≥8 視為刷滿整圈,原始分數=26×8=208。
右手第一次動,combo=1 → 208×1=208。
範例三:
第一次刷圈:左手 d=+4,路徑 2,3,4,5;原始分數=1+1+1+2=5;左手第一次,combo=1 → 5。
第二次刷圈:還是左手 d=+2,路徑 6,7;原始分數=2+2=4;方向同前一次左手,combo 變 2 → 4×2=8。
總分 5+8=13。
範例四:
第一次刷圈:左手 d=+3,路徑是 2,3,4,原始分數=2+3+4=9。左手第一次動,combo=1 → 得 9。
第二次刷圈:右手 d=-2,路徑是 8,7,原始分數=8+7=15。右手第一次動,combo=1 → 得 15。
第三次刷圈:左手 d=-4,路徑是 3,2,1,8,原始分數=3+2+1+8=14。方向與上次左手相反,combo=1 → 得 14。
第四次刷圈:右手 d=+5,路徑是 8,1,2,3,4,原始分數=8+1+2+3+4=18。方向與上次右手相反,combo=1 → 得 18。
第五次刷圈:左手 d=+1,路徑是 1,原始分數=1。方向與上次左手相反,combo=1 → 得 1。
第六次刷圈:右手 d=-1,路徑是 3,原始分數=3。方向與上次右手相反,combo=1 → 得 3。
總分 9+15+14+18+1+3=60。
| 編號 | 身分 | 題目 | 主題 | 人氣 | 發表日期 |
沒有發現任何「解題報告」 |
|||||