b234. P1 裝飲料 - 旦旦解題農場

內容

有一個杯子，可將其體積視為由兩個長方體組成（如下圖），下方的長方體底面積為 $w_1 * w_1 \; cm^2$，高為 $h_1 \; cm$，上方的長方體底面積為 $w_2 * w_2 \; cm^2$，高為 $h_2 \; cm$。

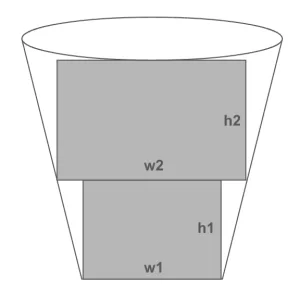
一開始杯子為空。要裝 $n$ 次飲料，每一次裝 $v \; cm^3$ 容量的飲料，當水杯滿時水位不再上升。問這 $n$ 次倒飲料中水位上升變化量最高是幾 $cm$。

輸入說明

第一列輸入一數 $n$，代表要裝 $n$ 次飲料。

第二列輸入 $4$ 個數 $w_1 , w_2 , h_1 , h_2$，代表杯子的寬度與高度。

第三列有 $n$ 個 $v$ 代表每次裝飲料的容量。

輸出說明

輸出上升變化量最大的高度為何。

範例輸入

範例一:
1
4 6 8 5
200
------
範例二:
2
5 10 12 8
400 600

範例輸出

範例一:
10
------
範例二:
13

測資資訊：

記憶體限制： 64 MB
公開測資點#0 (10%): 1.0s , <1K
公開測資點#1 (10%): 1.0s , <1K
公開測資點#2 (10%): 1.0s , <1K
公開測資點#3 (10%): 1.0s , <1K
公開測資點#4 (10%): 1.0s , <1K
公開測資點#5 (10%): 1.0s , <1K
公開測資點#6 (10%): 1.0s , <1K
公開測資點#7 (10%): 1.0s , <1K
公開測資點#8 (10%): 1.0s , <1K
公開測資點#9 (10%): 1.0s , <1K

提示：

保證每次水位上升都是整數。

$60\;\% : n = 1 \; , \; 1 \leq w_1 , w_2 , h_1 , h_2 \leq 50$

$100\;\% : 1\leq n \leq 10 \; , \; 1 \leq w_1 , w_2 , h_1 , h_2 \leq 50$

範例一:

第一次倒第一杯裝滿，水還剩 $72 \; cm^3$ ，會在第二杯上升 $2 \; cm$ ，共上升 $8 + 2 = 10 \; cm$。

範例二:

第一次倒第一杯裝滿，水還剩 $100 \; cm^3$ ，會在第二杯上升 $1 \; cm$ ，共上升 $12 + 1 = 13 \; cm$ ，第二杯還剩 $700 \; cm^3$。

第二次倒第二杯上升 $6 \; cm$。

第一次上升比較大。

題解。

標籤:

教學用

出處:

APCS 2024.10.20 [管理者：

Pote_Liu (13th 初階助教)

]

編號	身分	題目	主題	人氣	發表日期
沒有發現任何「解題報告」